Axiomatic validation of memory barriers and atomic instructions

Although memory barriers and atomic instructions are less obscure than they once were, they can still be rather confusing. The need for atomic instructions is easy to see: if multiple CPUs execute a++ simultaneously, some increments could be lost. For example, if the initial value of a was zero, then all (say) eight CPUs might concurrently load zero, add one to it, and then all store the value one, rather than the correct value of eight. In contrast, atomic_inc(&a) would faithfully record each and every increment to a.

To see the need for memory barriers, keep in mind that both the compiler and the CPU can cause memory-reference instructions to be reordered. It is important to remember that even strongly ordered systems such as x86 and the IBM Mainframe still do some reordering, namely, allowing prior stores to be executed after subsequent loads. For example, consider the following x86 litmus test, with x and y both initially zero:

    CPU 0		CPU 1
    -----		-----
    mov [x],$1		mov [y],$1
    mov eax,[y]		mov eax,[x]

It is possible for both CPUs' eax registers to be equal to zero at the end of this test, because both of the loads can be executed before either of the stores. (In fact, this outcome could occur even if just one of the loads was executed before both stores.) To prevent this reordering, we can insert mfence instructions as follows:

    CPU 0		CPU 1
    -----		-----
    mov [x],$1		mov [y],$1
    mfence		mfence
    mov eax,[y]		mov eax,[x]

These added mfence instructions ensure that at least one of the CPUs will end up with a non-zero eax register.

But this leads to the question: “Exactly where do I need to place memory-barrier instructions?” For most developers, even Linux kernel hackers, the answer is “Nowhere.” The reason for this reassuring answer is that most synchronization primitives already contain the needed memory barriers. Therefore, if you use locks, sequence counters, atomic operations, or read-copy-update (RCU) in the intended manner, you don't need to add any explicit memory-barrier instructions. Instead, the required memory-barrier instructions are included in these synchronization primitives.

Of course, if you are writing tricky code (in which case, you should think twice) or if you are writing your own synchronization primitive (in which case you should also think twice), you will need to add your own memory barriers and atomic instructions. One indispensable source of help is the documentation in Documentation/atomic_ops.txt and Documentation/memory-barriers.txt. You most definitely need to read and understand these documents before using atomic operations or explicit memory-barrier instructions.

armmem/ppcmem tool

Once you have read this documentation, another source of help is the armmem/ppcmem tool discussed in an LWN article that appeared in 2011. This tool has been extremely helpful for validating short sequences of critical code for the Linux kernel and elsewhere; however, it can be a bit slow. For example, consider the “independent reads of independent writes” (IRIW) litmus test, in which one thread (call it “P0”) writes the value 1 to variable x, another thread (P1) writes the value 1 to variable y, a third thread (P2) reads x then y separated by a full barrier, and a fourth thread (P3) reads these two variables in the opposite order. Both x and y are initially zero. The corresponding PowerPC litmus test is as follows:

 1 PPC IRIW.litmus
 2 ""
 3 (* Traditional IRIW. *)
 4 {
 5 0:r1=1; 0:r2=x;
 6 1:r1=1;         1:r4=y;
 7         2:r2=x; 2:r4=y;
 8         3:r2=x; 3:r4=y;
 9 }
10  P0           | P1           | P2                 | P3                 ;
11  stw r1,0(r2) | stw r1,0(r4) | lwz r3,0(r2)       | lwz r3,0(r4)       ;
12               |              | sync               | sync               ;
13               |              | lwz r5,0(r4)       | lwz r5,0(r2)       ;
14 
15 exists
16 (2:r3=1 /\ 2:r5=0 /\ 3:r3=1 /\ 3:r5=0)

Line 1 identifies this as a PowerPC litmus file, and gives it the name “IRIW.litmus”. An ARM litmus file would, of course, substitute “ARM” for the above “PPC”. Line 2 provides a place for an alternative name for the test, which you will usually want to leave blank as shown. Comments may be inserted at this point, as shown on line 3, using the OCaml (or Pascal) syntax of “(* *)”. These comments can span multiple lines if desired.

Lines 4-9 provide initial values for the machine registers, and are of the form “P:R=V”, where “P” is the process identifier, “R” is the register identifier, and “V” is the value. For example, Process P0's register r1 initially contains the value 1, and its register r2 initially contains the address of variable x. Uninitialized variables default to the value zero, so that, in the example, x and y are both initially zero. If desired, x and y can be initialized as well, for example, adding a “x=1; y=2;” after line 4 would initialize x to the value one and y to the value two.

Line 10 provides identifiers for the four processes, and must be of the form “PN” numbered consecutively starting from zero. Strict, perhaps, but it does help avoid confusion.

Lines 11-13 contain the code, so that P0 and P1 do their respective stores, and P2 and P3 do their loads in opposite orders, separated by a full memory barrier in the form of a sync instruction.

Finally, lines 15 and 16 contain the assertion, which in this case will trigger if P2 and P3 see the two stores from P0 and P1 happening in different orders.

Running this example using the full state-space search tool ppcmem gives the correct answer, namely that the assertion cannot fire. Automatic computation of this result is a great improvement over the alternative of poring over manuals and, in fact, armmem/ppcmem has been an invaluable aid in tracking down several Linux kernel issues over the past few years. However, armmem/ppcmem does take about 14 CPU hours to compute this result, and also requires about 10GB of main memory to hold the state space. Of course, 14 hours is a great improvement over the weeks or months required by manual methods, but these two kernel hackers are impatient and prize quicker answers to hard questions.

herd tool

Jade Alglave and Luc Maranget, who were members of the original group behind ppcmem, were joined by Michael Tautschnig in some recent work [PDF] that replaces the full state-space search with an axiomatic, event-based approach. This axiomatic approach can greatly reduce the time required to analyze a particular code fragment because its use of partially ordered relations means that it does not need to examine large numbers of equivalent, totally ordered sequences of states. Instead, the axiomatic approach constructs the set of possible candidate executions, rejecting those that do not meet the constraints of the underlying memory model. In herd, a candidate execution consists of little more than a mapping giving, for each load, the store that provided the memory value that was read. This compact representation results in a much smaller number of candidate executions than are considered by the full-state-space approach used by armmem/ppcmem, which should allow herd to run somewhat faster.

Running herd (as in “herd -model ppc.cat IRIW.litmus -o /tmp” after downloading from here or via  https://github.com/herd/herdtools) on the IRIW litmus test file gives the following output, which, like ppcmem, confirms that the assertion can never fire (note the second-to-last line beginning with “Observation”):

Test IRIW Allowed
States 15
2:r3=0; 2:r5=0; 3:r3=0; 3:r5=0;
2:r3=0; 2:r5=0; 3:r3=0; 3:r5=1;
2:r3=0; 2:r5=0; 3:r3=1; 3:r5=0;
2:r3=0; 2:r5=0; 3:r3=1; 3:r5=1;
2:r3=0; 2:r5=1; 3:r3=0; 3:r5=0;
2:r3=0; 2:r5=1; 3:r3=0; 3:r5=1;
2:r3=0; 2:r5=1; 3:r3=1; 3:r5=0;
2:r3=0; 2:r5=1; 3:r3=1; 3:r5=1;
2:r3=1; 2:r5=0; 3:r3=0; 3:r5=0;
2:r3=1; 2:r5=0; 3:r3=0; 3:r5=1;
2:r3=1; 2:r5=0; 3:r3=1; 3:r5=1;
2:r3=1; 2:r5=1; 3:r3=0; 3:r5=0;
2:r3=1; 2:r5=1; 3:r3=0; 3:r5=1;
2:r3=1; 2:r5=1; 3:r3=1; 3:r5=0;
2:r3=1; 2:r5=1; 3:r3=1; 3:r5=1;
No
Witnesses
Positive: 0 Negative: 15
Condition exists (2:r3=1 /\ 2:r5=0 /\ 3:r3=1 /\ 3:r5=0)
Observation IRIW Never 0 15
Hash=41423414f4e33c57cc1c9f17cd585c4d

However, instead of taking 14 hours to compute this result, herd completes in about 16 milliseconds, representing a speedup in excess of 3,000,000x, which is something that you do not see every day. (The herd paper claims only a 45,000x speedup.) However, it is only fair to add that ppcmem/armmem was implemented in a deliberately straightforward way, without performance optimizations, in order to increase the probability that it was in fact implementing the intended memory model, a point that is also called out on pages 3 and 61 of the herd paper.

The tool also reports assertion violations. For example, substituting the lightweight-barrier lwsync instruction for the full-barrier sync instruction gives the following output:

Test IRIW Allowed
States 16
2:r3=0; 2:r5=0; 3:r3=0; 3:r5=0;
2:r3=0; 2:r5=0; 3:r3=0; 3:r5=1;
2:r3=0; 2:r5=0; 3:r3=1; 3:r5=0;
2:r3=0; 2:r5=0; 3:r3=1; 3:r5=1;
2:r3=0; 2:r5=1; 3:r3=0; 3:r5=0;
2:r3=0; 2:r5=1; 3:r3=0; 3:r5=1;
2:r3=0; 2:r5=1; 3:r3=1; 3:r5=0;
2:r3=0; 2:r5=1; 3:r3=1; 3:r5=1;
2:r3=1; 2:r5=0; 3:r3=0; 3:r5=0;
2:r3=1; 2:r5=0; 3:r3=0; 3:r5=1;
2:r3=1; 2:r5=0; 3:r3=1; 3:r5=0;
2:r3=1; 2:r5=0; 3:r3=1; 3:r5=1;
2:r3=1; 2:r5=1; 3:r3=0; 3:r5=0;
2:r3=1; 2:r5=1; 3:r3=0; 3:r5=1;
2:r3=1; 2:r5=1; 3:r3=1; 3:r5=0;
2:r3=1; 2:r5=1; 3:r3=1; 3:r5=1;
Ok
Witnesses
Positive: 1 Negative: 15
Condition exists (2:r3=1 /\ 2:r5=0 /\ 3:r3=1 /\ 3:r5=0)
Observation IRIW Sometimes 1 15
Hash=a886ed63a2b5bddbf5ddc43195a85db7

This confirms that full barriers are required in order to prevent the assertion from firing: Compare the “Sometimes” on the second-to-last line of the output for lwsync to the “Never” on that same line in the previous output. This means that in the version of this litmus test using the sync instruction, the assertion can “Never” happen, while in the version using the lwsync instruction, it “Sometimes” can. Although this is nice to know, it would be even nicer to understand how the lwsync barriers allow this result to happen. Such understanding can be used to drive an interactive ppcmem/armmem session, providing a useful cross-check of herd's results. (And performance is not an issue when you are interactively studying a single path of execution rather than conducting a full state-space search.)

And that is what the “-graph cluster -show prop” arguments to the herd command are for. This generates a graphviz dot file as follows:

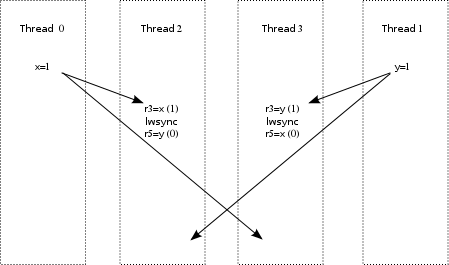
This diagram shows that while the lwsync instructions enforce the order of the individual reads, they do not force the writes to be propagated in the same order to Thread 2 and Thread 3. This may not be a surprise, but it is still nice to see it in diagram form. The labels on the arrows are defined as follows:

• fr: From read, which connects earlier loads to later stores at the same address, for example, from Thread 3's read of x to Thread 0's later write to this same variable.

• GHB: Global happens before, which is based on the effects of memory-barrier instructions and dataflow dependencies, illustrating the limited transitivity (aka “cumulativity”) of the lwsync instruction.

• po: Program order, for example, between the pairs of reads.

• propbase: Base store-propagation relationship that the herd tool uses to construct the full set of store-propagation relationships.

• rf: Read from, for example from the store to x to the load that returns the value written by that store.

The herd tool handles PowerPC and a few variants of ARM, as well as x86, a fragment of the C++ language (including its memory model), and several generations of NVIDIA GPUs, with the C++11 and GPU models having been supplied by Jade Alglave, Mark Batty, Luc Maranget, Daniel Poetzl, Tyler Sorensen and John Wickerson. In fact, one of the strengths of the herd tool is that it uses a very compact description of memory models, so that the ppc.cat file describing the PowerPC memory model is 67 lines long, and the x86tso.cat file describing the x86 memory model is only 23 lines long.

An example x86 litmus test follows, which was discussed on LKML in November 2013:

 1 X86 LockRelease
 2 ""
 3 { 
 4 x=0; y=0; z=0;
 5 }
 6  P0          | P1          | P2          ;
 7  MOV [x],$1  | MOV EAX,[z] | MOV [y],$1  ;
 8  MOV [z],$1  | MOV EBX,[y] | MFENCE      ;
 9              |             | MOV EAX,[x] ;
10 exists (1:EAX=1 /\ 1:EBX=0 /\ 2:EAX=0)

The incantation “./herd -model x86tso.cat x86-lock-barrier.litmus -o ~/tmp” gives the following output:

Test LockRelease Allowed
States 7
1:EAX=0; 1:EBX=0; 2:EAX=0;
1:EAX=0; 1:EBX=0; 2:EAX=1;
1:EAX=0; 1:EBX=1; 2:EAX=0;
1:EAX=0; 1:EBX=1; 2:EAX=1;
1:EAX=1; 1:EBX=0; 2:EAX=1;
1:EAX=1; 1:EBX=1; 2:EAX=0;
1:EAX=1; 1:EBX=1; 2:EAX=1;
No
Witnesses
Positive: 0 Negative: 7
Condition exists (1:EAX=1 /\ 1:EBX=0 /\ 2:EAX=0)
Observation LockRelease Never 0 7
Hash=98f5658ae7325da4775b1358920d466a

This is in agreement with the verdict from Intel's CPU architects—and herd delivered this verdict after a delay that extended for a full eleven milliseconds.

Linked data structures

It turns out that both ppcmem/armmem and herd can handle simple linked data structures, namely a singly linked list with no data. This makes it possible for these tools to validate some simple uses of RCU, for example, the 3-light scenario in the LWN article on the RCU-barrier menagerie:

 1 PPC RCU-3-tmp
 2 ""
 3 (* https://lwn.net/Articles/573497/ Scenario 3-light for Power.
 4    Also adds a temporary. *)
 5 {
 6 0:r0=1; 0:r3=x; 0:r4=y; 0:r5=z;
 7 1:r0=1; 1:r3=x; 1:r4=y; 1:r5=z;
 8 }
 9  P0             | P1            ;
10   lwz r6,0(r3)  | stw r0,0(r4)  ;
11   cmpwi r6,0    | lwsync        ;
12   beq Fail      | stw r4,0(r3)  ;
13   stw r6,0(r5)  |               ;
14   lwz r8,0(r5)  |               ;
15   lwz r7,0(r8)  |               ;
16  Fail:          |               ;
17 
18 exists
19 (0:r6=y /\ 0:r7=0)

Processor P1 initializes the new node (which is variable y) on line 10 and does an rcu_assign_pointer() into the list header (which is variable x) on lines 11 and 12. Variable x now contains a pointer to variable y, which in turn contains the value one. Meanwhile, processor P0 does an rcu_dereference() (line 10), checks for a NULL pointer (lines 11 and 12), stores the resulting non-NULL pointer to a temporary (line 13), loads the pointer back from the temporary (line 14), and finally loads the contents of the first element in the list.

If the value returned from rcu_dereference() is a pointer to y, but dereferencing that pointer returns a value of zero, we are in trouble. Therefore, the condition on line 19 should never happen. And, fortunately, both tools agree that it never does:

Test RCU-3-tmp Allowed
States 2
0:r6=0; 0:r7=0;
0:r6=y; 0:r7=1;
No
Witnesses
Positive: 0 Negative: 2
Condition exists (0:r6=y /\ 0:r7=0)
Observation RCU-3-tmp Never 0 2
Hash=413c6e17f142bfa3835ed993c8ebf814

There is some work in progress to handle more complex data structures — though, in the words of one of the researchers: “Don't hold your breath!” Nevertheless, the above litmus test shows that even this limited ability to handle single-member data structures can be quite useful.

Scalability

We already saw that herd is blindingly fast, but it is still interesting to look at its scalability. Two tests will demonstrate this, the first being an extension of the IRIW litmus test discussed above. This test is augmented so that the writing processors do additional (useless) writes, so that the five-writes-per-processor litmus test appears as follows:

 1 PPC IRIW5.litmus
 2 ""
 3 (* Traditional IRIW, but with five stores instead of just one. *)
 4 {
 5 0:r1=1; 0:r2=x;
 6 1:r1=1;         1:r4=y;
 7         2:r2=x; 2:r4=y;
 8         3:r2=x; 3:r4=y;
 9 }
10  P0           | P1           | P2                 | P3                 ;
11  stw r1,0(r2) | stw r1,0(r4) | lwz r3,0(r2)       | lwz r3,0(r4)       ;
12  addi r1,r1,1 | addi r1,r1,1 | sync               | sync               ;
13  stw r1,0(r2) | stw r1,0(r4) | lwz r5,0(r4)       | lwz r5,0(r2)       ;
14  addi r1,r1,1 | addi r1,r1,1 |                    |                    ;
15  stw r1,0(r2) | stw r1,0(r4) |                    |                    ;
16  addi r1,r1,1 | addi r1,r1,1 |                    |                    ;
17  stw r1,0(r2) | stw r1,0(r4) |                    |                    ;
18  addi r1,r1,1 | addi r1,r1,1 |                    |                    ;
19  stw r1,0(r2) | stw r1,0(r4) |                    |                    ;
20 
21 exists
22 (2:r3=1 /\ 2:r5=0 /\ 3:r3=1 /\ 3:r5=0)

The time required as a function of the number of per-thread writes is as follows:

Writes Per Processor	Time (s)	Relative Slowdown	Slowdown vs. 1 Write
1	0.017
2	0.152	8.9x	8.9x
3	1.940	12.8x	114.1x
4	25.182	13.0x	1,481.3x
5	984.798	39.1x	57,929.3x

So although herd is quite fast compared to full-state-space search, it is still most emphatically exponential. However, one of the reasons for the slowness is that “./herd -model ppc.cat” calculates all possible coherence orders (orders of writes to a given single variable), even those that do not matter to the reads. However, herd provides an alternative memory model that computes only the subset of the coherence order that actually matters to readers. Substituting this alternative “prettycat.cat” model for “ppc.cat” runs the five-write-per-processor litmus test in 3.888 seconds, which is a few orders of magnitude faster than the 984.798 seconds that ppc.cat manages. Of course, as with other software tools, adding optimization adds risk!

The second test chains the WWC+lwsyncs litmus test, but instead of extending the number of writes per processor, extends the number of processors. Here is the base-level three-processor version:

 1 PPC WWC+lwsyncs
 2 "Rfe LwSyncdRW Rfe LwSyncdRW Wse"
 3 Cycle=Rfe LwSyncdRW Rfe LwSyncdRW Wse
 4 {
 5 0:r2=x;
 6 1:r2=x; 1:r4=y;
 7 2:r2=y; 2:r4=x;
 8 }
 9  P0           | P1           | P2           ;
10  li r1,2      | lwz r1,0(r2) | lwz r1,0(r2) ;
11  stw r1,0(r2) | lwsync       | lwsync       ;
12               | li r3,1      | li r3,1      ;
13               | stw r3,0(r4) | stw r3,0(r4) ;
14 exists
15 (x=2 /\ 1:r1=2 /\ 2:r1=1)

In C, this looks something like the following (but in real life, don't forget the ACCESS_ONCE() calls!):

 1 CPU 0          CPU 1          CPU 2
 2 -----          -----          -----
 3 x = 2;         r1 = x;        r2 = y;
 4                lwsync();      lwsync();
 5                y = 1;         x = 1;
 6 
 7 assert(!(x==2 && r1==2 && r2==1));

This can be extended to add a fourth processor as follows:

 1 PPC WWC4+lwsyncs
 2 "Rfe LwSyncdRW Rfe LwSyncdRW Wse"
 3 Cycle=Rfe LwSyncdRW Rfe LwSyncdRW Wse
 4 {
 5 0:r2=x;
 6 1:r2=x; 1:r4=y;
 7 2:r2=y; 2:r4=z;
 8 3:r2=z; 3:r4=x;
 9 }
10  P0           | P1           | P2           | P3           ;
11  li r1,2      | lwz r1,0(r2) | lwz r1,0(r2) | lwz r1,0(r2) ;
12  stw r1,0(r2) | lwsync       | lwsync       | lwsync       ;
13               | li r3,1      | li r3,1      | li r3,1      ;
14               | stw r3,0(r4) | stw r3,0(r4) | stw r3,0(r4) ;
15 exists
16 (x=2 /\ 1:r1=2 /\ 2:r1=1 /\ 3:r1=1)

Which looks something like the following in C:

 1 CPU 0          CPU 1          CPU 2          CPU 3
 2 -----          -----          -----          -----
 3 x = 2;         r1 = x;        r2 = y;        r3 = z;
 4                lwsync();      lwsync();      lwsync();
 5                y = 1;         z = 1;         x = 1;
 6 
 7 assert(!(x==2 && r1==2 && r2==1 && r3 == 1));

This test continues adding processors up through 12 processors, resulting in this monstrosity, which is best viewed in full-screen mode. Surprisingly, herd deals just fine with twelve threads. And although herd still shows exponential behavior, the slowdowns are considerably milder than for the previous augmented IRIW example:

Threads	Time (s)	Relative Slowdown	Slowdown vs. 3 Processors
3	0.017
4	0.023	1.4x	1.4x
5	0.049	2.1x	2.9x
6	0.107	2.2x	6.3x
7	0.255	2.4x	15.0x
8	0.613	2.4x	36.1x
9	1.471	2.4x	86.5x
10	3.444	2.3x	202.6x
11	7.938	2.3x	466.9x
12	17.711	2.2x	1,041.8x

In short, herd appears to be able to handle most reasonably sized litmus tests with eminently reasonable runtime. Perhaps surprisingly, herd seems happier with multiple processors than with multiple writes to the same memory location.

Limitations and summary

However, it is important to consider some intrinsic limitations of the herd tool, which are similar to those of ppcmem/armmem:

1. These tools do not constitute official statements by ARM, IBM, or Intel on their respective CPU architectures. For example, all three corporations reserve the right to report a bug at any time against any version of any of these tools. These tools are therefore not a substitute for careful stress testing on real hardware. Moreover, both the tools and the model that they are based on are under active development and might change at any time.
2. Contrariwise, at least one counterexample (observed on real hardware) to the results reported by the tools has been recognized by the official architects as demonstrating a silicon bug. The processors are also under active development.
3. ppcmem/armmem on the one hand and herd on the other do not always agree. These tools do give the same results for each litmus test in a suite of more than 8,000 such tests; however, there are a couple of examples where they differ. One example is Figure 37 of the herd paper, and Alan found a smaller example. Both examples are quite obscure. But there is a formal result in one direction; Section 7.3 of the paper (pages 45-49) contains a proof that whenever ppcmem/armmem believes an assertion can be triggered, herd will report the same. In other words, herd is more conservative: it may indicate that a litmus test contains a synchronization error even though ppcmem/armmem thinks the test is okay. Nevertheless, when either one reports a possible assertion violation, it is wise to use the tools' reporting and visualization capabilities to help understand the reason for the violation.
4. The herd tool is still exponential in nature, though much much faster than its predecessors.
5. Neither armmem/ppcmem nor herd is much good for complex data structures, although you can create and traverse super-simple linked lists using initialization statements of the form “x=y; y=z; z=42;”.
6. Neither armmem/ppcmem nor herd handles memory-mapped I/O or device registers. Although there might come a time when we have formal models not only of normal memory, but of I/O devices as well, now is not yet that time.
7. The tools will detect only those problems for which you code an assertion. This weakness is common to all formal methods, and is yet another reason why testing remains important. In the immortal words of Donald Knuth: “Beware of bugs in the above code; I have only proved it correct, not tried it.”

On the other hand, one nice thing about tools such as ppcmem/armmem and herd is that they are designed to model the full range of behaviors permitted by the architecture. This full range includes behaviors that current hardware does not exhibit, but which future hardware might. Use of these tools is thus one good way to future-proof your code.

All that said, it is best to design your code to be easily partitioned and to use higher-level synchronization primitives such as locks, sequence counters, atomic operations, and RCU. But for those of us who design and implement these synchronization primitives, ppcmem/armmem and herd are likely to be quite helpful.

Acknowledgments

We owe thanks to H. Peter Anvin (and the anonymous Intel CPU architects) who validated the x86 litmus test, and to Richard Grisenthwaite and Derek Williams for many helpful discussions of the ARM and the Power architectures, respectively. We are all indebted to Luc Maranget, Jade Alglave, Peter Sewell, and Susmit Sarkar for their review of an early draft of this article. We are grateful to Jim Wasko for his support of this effort.

Answers to Quick Quizzes

Quick Quiz 1: Why can't the CPU designers simply make their hardware do things in order???

Answer: Because full ordering destroys performance and scalability. This reordering of earlier stores against later loads allows the hardware to buffer stores, so that a long series of stores need not force the hardware to stall while waiting for ownership of the corresponding cache lines to make its way to the CPU doing the stores. In fact, thread-local reordering is just the beginning: compilers can also eliminate and introduce memory accesses, and in the Power and ARM architectures different writes by a given processor can propagate to the other processors in different orders.

Back to Quick Quiz 1.

Quick Quiz 2: But the diagram has a cycle involving the two fr arrows! How can that possibly happen? Do these computer systems have some sort of built-in time machine???

Answer: The hardware uses exactly the same time machine that we all use, namely the one that propels us into the future at a rate of one second per second. To see how that cycle can happen, imagine a system where Thread 0 and Thread 2 are close to each other, for example, they might be a pair of hardware threads running in the same CPU core. Imagine that Thread 1 and Thread 3 are similarly close to each other. This could cause Thread 2's loads to become aware of Thread 0's store much more quickly than Thread 3's loads do, as shown in the following diagram, with time advancing from top to bottom.

As you can see, this “counter-intuitive” result can be explained by simple propagation delay. The question of how sync instructions manage to prevent executions like this one is left as an open exercise for advanced students.

Back to Quick Quiz 2.

Quick Quiz 3: How could anyone possibly describe something as complex as a memory model in only 23 lines of text?

Answer: By using high-level notation, for example as follows for x86:

"X86 TSO"

(* Uniproc check *)
let com = rf | fr | co
acyclic po-loc | com

(* Atomic *)
empty atom & (fre;coe)

(* GHB *)
#ppo
let po_ghb = WW(po) | RM(po)

#implied barriers
let poWR = WR(po)
let i1 = PA(poWR)
let i2 = AP(poWR)
let implied = i1 | i2

let GHB = mfence | implied | po_ghb | rfe | fr | co
show mfence
show implied
acyclic GHB

This might serve as a useful reminder that “concise” and “easy to read” are orthogonal concepts. On the other hand, the 23 lines include both blank lines and comments. The notation is explained in the herd paper.

Back to Quick Quiz 3.

Quick Quiz 4: What kind of locking primitive gets away without using atomic instructions, anyway???

Answer: High-contention handoff of a queued locking primitive.

Now, the initial acquisition of a queued lock does in fact use atomic instructions, as it must to handle the possibility of multiple CPUs concurrently attempting to acquire the lock at a time when no CPU holds it. However, the high-contention handoff is from the CPU holding the lock to the CPU that is first in line to acquire it. Because there are only two CPUs involved, atomic instructions are not needed.

This should come as no surprise, as the classic single-producer/single-consumer array-based FIFO implementation also needs no atomic instructions, and for the same reason.

Back to Quick Quiz 4.